I’ve begun in earnest to build the Checkers AI, and right now for the most part that means plumbing. Before I even get to how this NN is going to work, I need to have the framework in place that will be able to represent and play the games. I’ve also begun to think through some of the reinforcement learning models — something I readily admit, I don’t have any real expertise in. But let’s start with the “boring” stuff.

The Plumbing

First, assuming this is something that will eventually be worth sharing, I have started a Github repository. That can be found here.

More to the point though, I have started to model the board representation. As discussed previously, for checkers, the board is fundamentally 8×4, and the starting position for the board is with 12 red and 12 black pieces in their appropriate starting locations.

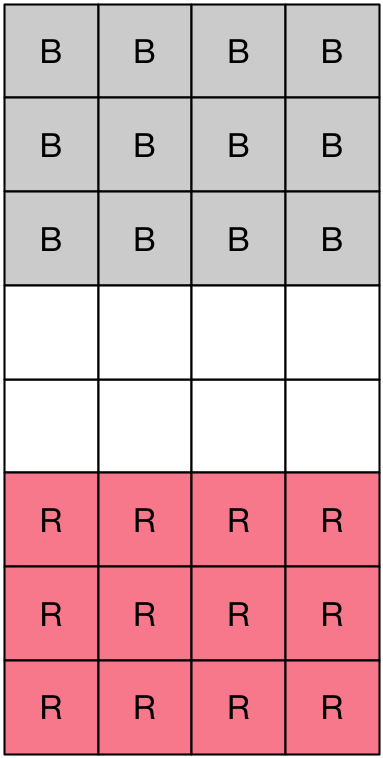
Originally, I had the idea that for inputs, I would use five mutually exclusive inputs including unoccupied. Thinking it over, it makes more sense to have four positive states—Red, Black, Red King, and Black King (R, B, RK, BK)—and unoccupied will be represented by having all those inputs at zero.

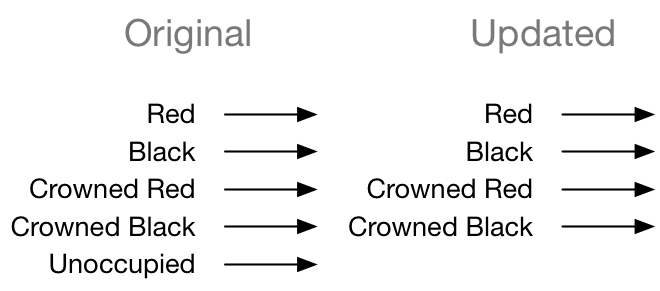
Mapping each of those inputs to a layer of the board, we have this as the representation of the initial board position:

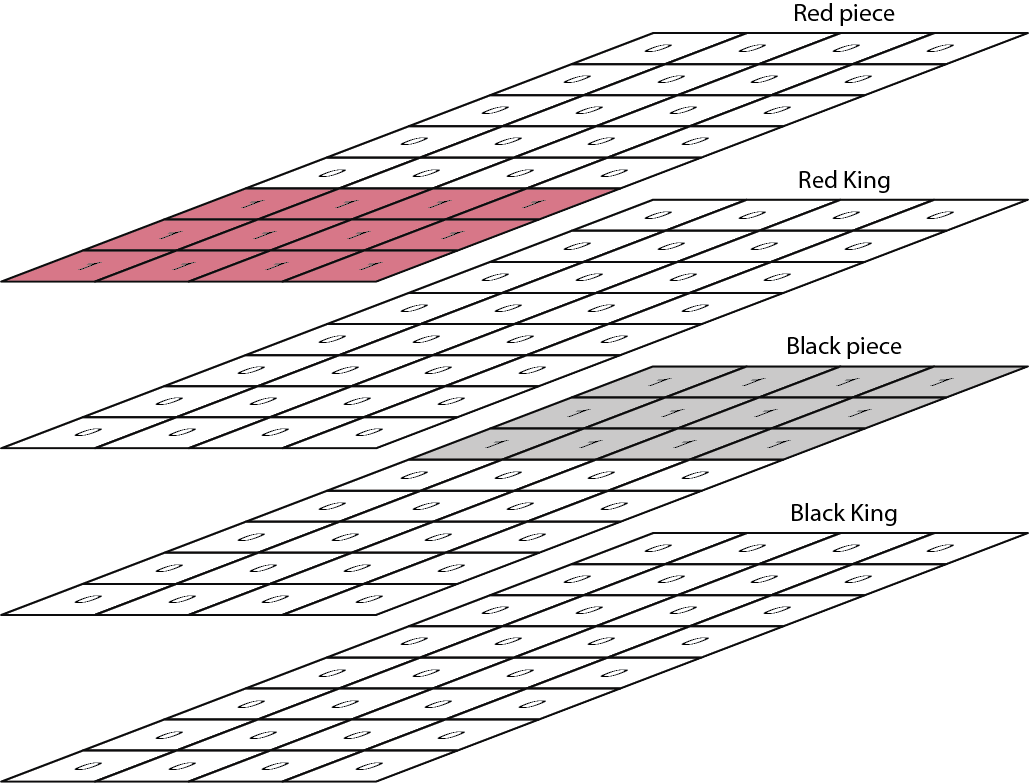
It’s a 3 dimensional matrix (4,8,4). The first dimension represents the four layers (R, B, RK, BK).

I’ve thought a good deal about whether this is ideal or not. It seems like this could be compressed somewhat since considering each layer in a position as a boolean state, I’m effectively using four bits to accomplish what could be accomplished in three. However, memory is clearly not a constraint, and there are not any obvious inefficiencies in this representation. However, it seems possible that compressing each position into a single input with many different values could have a significant impact on the size of the various matrices of whatever NN I design, and hence the calculations necessary. At this point, though, I know for sure that I’m getting a clean signal. Once I’ve built the overall algorithms, I can experiment with dealing with the inputs differently.