Back in this post I alluded to the fact that I hadn’t yet written out the approach I’m going to use to calculate costs not just for a single output as in Andrej Karpathy’s Pong from Pixels but from 48 outputs representing 12 pieces with 4 possible moves for each, not all of them legal. Here is my current plan, and the hypotheses behind each component of that plan.

Hypothesis: Use Softmax on the Output Nodes

Karpathy uses a sigmoid activation function on his single output node. This makes sense for his single output because at its core, it’s easy to see his single output node as needing to classify his single output in terms of a single probability: the probability that the paddle will move down.

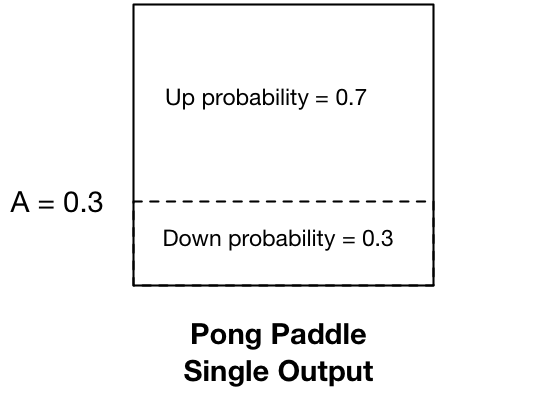
If it doesn’t move down, it moves up, since for simplicity sake, he doesn’t build the possibility of staying still. And he describes it both in his blog post and the python comments (“# roll the dice!”) in exactly those terms.

Looked at in that way, my challenge is similar, except that I have 48 possible outputs. But ultimately, I want to know the probability for each output for the player to “roll the dice” according to the probabilities of each possible output move. The multi class variant of sigmoid which I’ll use for my 48 output array is Softmax which generates a probability for each output which over the set of outputs sums to 1 (or 100%). To the extent that it’s a classifier, this makes sense.

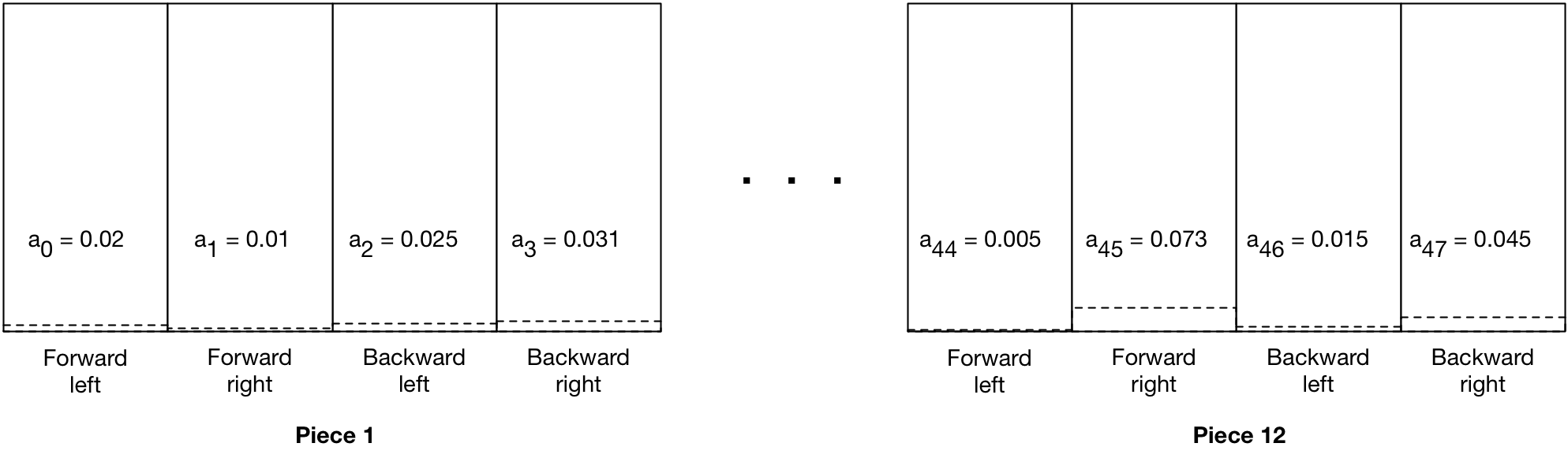
However there seem to be some wrinkles to what I’m trying to do that are not factors in what Karpathy is doing. And additionally, there are ways to look at this which are fundamentally different than a classification problem. For instance, in a classifier, we’d be comparing the outputs to labels which would be one-hot representations that a) have a only two possible values, 1 and 0, and b) will always sum to 100%. As I’ll get to subsequently, neither of these are necessarily the case in what I’m doing here. For these reasons, softmax remains merely my best hypothesis at this point.