It’s been an eventful few days for my model. This entry is going to be a bit of a saga, but here goes.

I had implemented the weighting function as described in my last post. I was getting great results right up until the percentage got to between 92 and 93 percent. Then progress would stall, get noisy, and not really go anywhere.

Same for the cost as you can see.

This was disheartening. It made me consider this whole pursuit. Learning legal moves was not even a primary goal for this project. It was simply a good starting point for getting familiar with a new type of training, a new type of learning, and working with hand-coded models myself. So I just didn’t (and don’t) want to get too bogged down in the particulars. So I had a thought: everything I’m doing right now is testing on probabilistically generated moves. That is, the model generates a random choice of moves corresponding to the probabilities of each output. But how about this: after training the model as far as it would go, what would the illegal moves percentage look like if I just picked the highest probability output, and if that didn’t work, the next highest, etc. until a legal move? Maybe I’d be at 50 percent.

My hope was that I would be able to at least declare a limited victory and move on. But then a funny thing happened. Writing the code to choose the highest probability outputs was a little trickier than I thought, at least in part owing to my still developing NumPy skills. And while debugging the algorithm to make that new choice, I found a bug in how I was applying the weights from illegal moves. Specifically, in the one scenario where it gets the move on the first try, rather than applying a weight of 1, it would apply the weight of whatever the last move was. Thus if the last move took 7 or 50 or 100 attempts to get to a successful move, that weight would be applied not only to that last move (appropriately), but also to the perfect next move. Thus, that move which should be weighted at 1, would instead get weighted at 7 or 50 or 100. Could that have been why the model was stalling between 92 and 93 percent?

Yes. Yes it could.

After fixing that bug, suddenly the model would plow through that old barrier between 92 and 93 percent down into the mid and low 80’s:

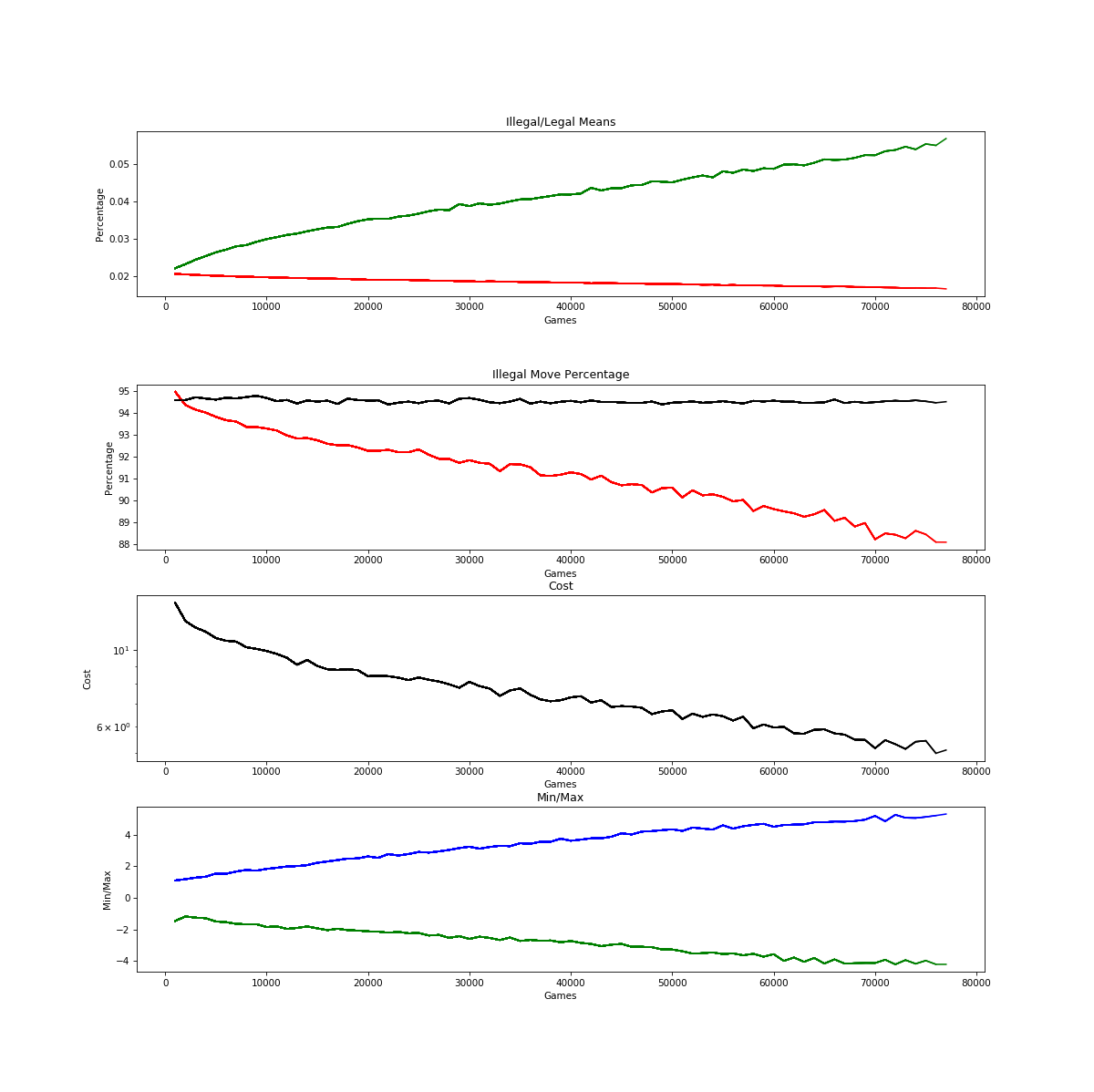
If you look at the “Percentage” graph above, you can see the percentage cruising, seemingly unabated and in fact accelerating a bit, through the eighties at around 80,000 games. But you will also note that the graph shown above stops before 80,000, and there is a new graph: Min/Max. These two observations reflect the fact that when the model starts to get into the low 80’s for percent of legal moves (usually around 100,000 games) it suffers complete and catastrophic failure.

I’m not talking about learning coming to a halt as it did with the bug in place. I’m not even talking about it reverting to random chance or worse than random chance over many, many batches as was happening before I build the cost weighting into the model in the first place. I’m talking about it making steady progress downward, and then over the course of just two training batches suddenly going from, say 82% illegal moves to almost 100% illegal moves. It’s basically the neural network equivalent of the plane suddenly just exploding mid-air for no apparent reason. And this didn’t just happen once. It happens consistently.

My initial worry was that, because I’m not using batch normalization on the linear output before the softmax, that I was overflowing the softmax function. The Min/Max graph above tracks the minimum and maximum linear outputs of the last layer that then feed the final softmax layer. Yes, as the network learns, they’re getting bigger, but they didn’t seem to be getting to a point that would overflow (or even underflow) the softmax algorithm. So I decided to track the linear outputs of all the layers (there are 6) over time. Here’s what that looked like in the games right before the explosion:

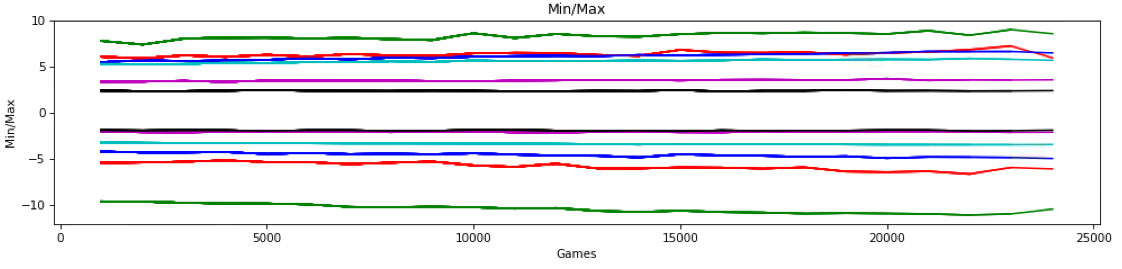
Note: this graph does not show the first ~25,000 games from a freshly initialized model. This shows the games after saving at about 70,000 games and starting from a checkpoint which resets the game counter. We see steady but slight decreases/increases in min/max for all of the six layers. But after the last training batch at 24,000 games, we see a slightly unusual perturbation, specifically in the max value of the linear output of the last layer (red, near the top) drops more than might be expected. And the min value of the second to last layer (green at the bottom) increases a bit more than would be expected. Here is the corresponding percentage graph:

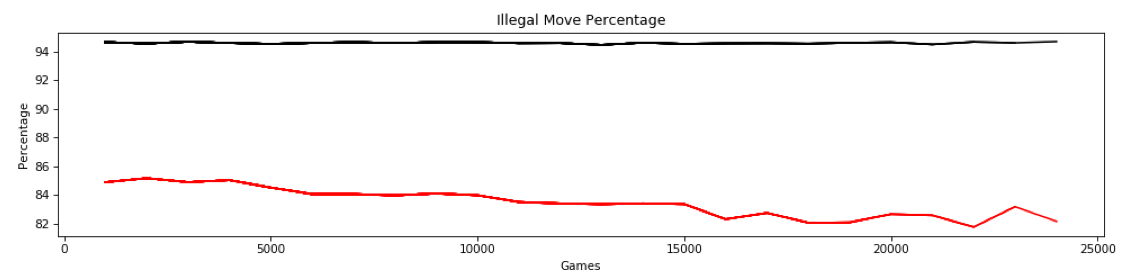
So we had an illegal move percentage for the last 1,000 games of around 83% which was well in line with the values we had been getting to that point. But for some reason, the training that occurred after that batch caused this slight perturbation. Here are the results of the next 1,000 games which would have incorporated the perturbation into the model for playing those games:

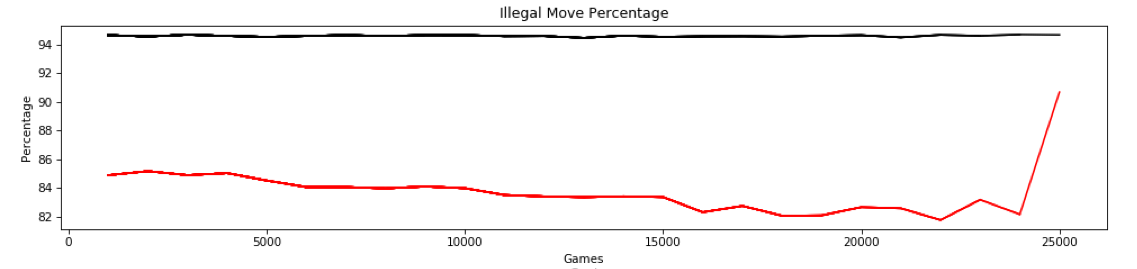
Boom. Suddenly the illegal move percentage is around 90%. This is reflected in the cost for that batch as well:

And so after playing that batch of 1,000 games, there was another round of training. After that training, here’s what happens to the min/max of the linear outputs of each layer using the last 1,000 games as input:

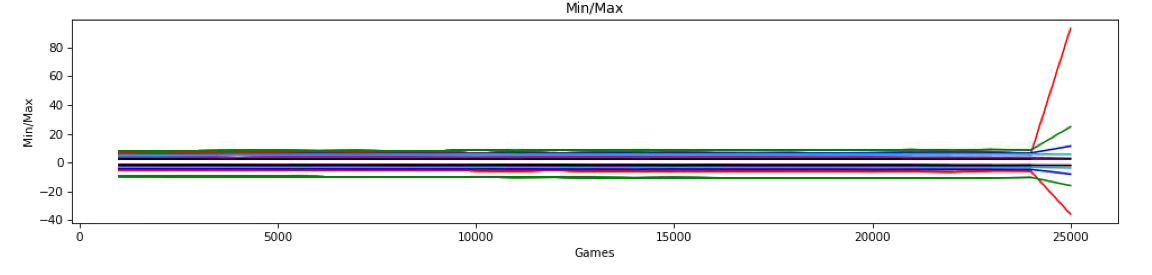
This is the explosion.

So we have a normal batch (83%) which causes our slight perturbation in the min/max linear output of a couple of the layers, which then causes the spike to 90%. Training the model on the batch that has that 90% spike in turn then causes the linear outputs (using the same 1,000 games as input) to go (almost) off the charts as shown above. Linear outputs like that would almost certainly be getting close to overflowing the softmax calculation. And after that training, even playing games ground to a halt. Ordinarily, the system can play approximately 10 games a second. With the outputs as shown (and whatever network parameters caused them) the machine takes well over a minute to play a single game. Clearly, the output probs are way, way, way out of whack.

I would have imagined that something would have had to cause the parameters to become grotesquely altered in order to get such a result in the linear outputs. But below are three graphs.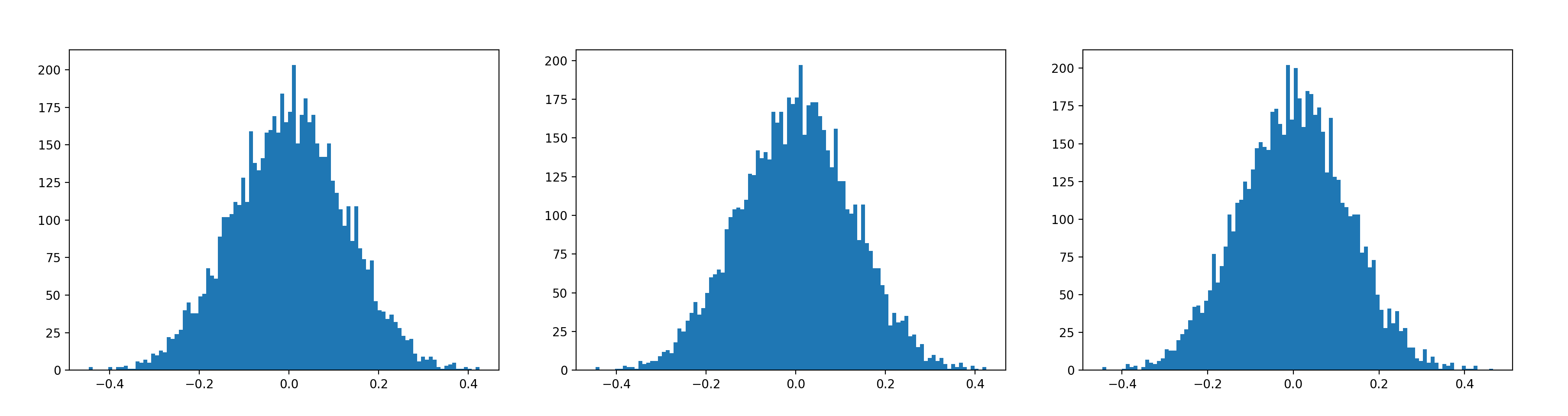

The first is the histogram of the W parameters feeding into the final layer about 25,000 games (25 batches) before the “explosion.” The second is the parameters after the appearance of the “perturbation.” The final is what things looked like after the linear output explosion. The difference between the second and the third (before and after the explosion, and merely one batch apart) is not qualitatively different from the difference between the first two, which are 25 batches apart. The other layers (not shown here) are even more similar. And yet that final one is basically the parameters of a completely broken model.

Where to Go from Here?

So here’s the thing. I’m actually dying to figure out what the problem is here. I have lots of ideas about how to investigate more deeply and get some real answers as well as some hypotheses on how to solve it (batch normalization?). I’m confident I can get to the bottom of it. It’s all I can do not to keep myself from going deeper down this rat hole.

But the thing is, it is a rat hole. The goal of this project has never been to have the AI learn legal moves. But it seemed like a great starting point for my first fully independent, hand-coded model, and one that diverged significantly in its intent and technique from anything we were taught in my coursework. It has served that function well. I have taught myself new approaches to problems, and even derived my own back propagation algorithm for Softmax. Now it’s time to move on to other more important forward looking goals.

I never thought my hand-coded, fully-connected neural network would succeed in learning to play checkers well. I have always assumed I’d be moving on to much more sophisticated networks (convolutional etc.) as well as more sophisticated optimization algorithms etc. And I never assumed that I’d be hand coding all of that, but instead would start using TensorFlow, Keras, and other powerful machine learning frameworks for that.

So it’s time for me to move away from this in earnest and start making progress in those other goals. Here’s the plan. I still would like to figure out what might fix this, but if it means hand-coding batch normalization, that’s way too time consuming. What I am willing to do, though, is add the one thing we learned about in the intro to machine learning course, but never implemented in Deep Learning and Neural Networks: regularization. I have a hunch that might fix this little explosion problem, and it’s really just a few minor changes to the code to add that.

So I’m going to do that in parallel to, now, starting to do a few tutorials on TensorFlow. My short term mini-project is, not unlike my mini-project from several months ago to learn Python, focused entirely on learning a new framework within a domain where I’ve already achieved success. I’m going to port my hand coded network, as is, to TensorFlow.