I’ve completed changing my code to support a model designed to win games rather than guess legal moves. The model is the same, but the reward function, some game details, and much of the administrative framework has changed.

The actual loss function is still Policy Gradient Loss. But now I am reinforcing with a +1 reward for moves made in a winning game, and -1 for moves made in a losing game rather than just +1 for legal moves.

I also decided to implement draw games. Part of the code I had was already set up for that, but in actual game play, all games were played until there was a a winner or loser. This has generally been fine. However, I noticed that as the model got trained to prefer winning moves and avoid losing moves, when games got to the point of there being just a couple of pieces for either side on the board, some games were taking seconds to complete. Looking at the move counts, it was because some games were going many thousands of moves before the probability distribution chose the “wrong” move.

So I set it up so than if more than 50 moves went by without a jump, the game would be called a draw and reward set to zero. It reduced the yield in terms of games because a good percentage of games in any 500-game batch would end in a draw and not reinforce the model one way or the other.

The most important change I made was the addition of the bootstrap framework. I set it up so that at the start, there would be two different initialized versions of the same model (red_model and black_model) competing against one another. However, red_model would be trained after each batch and the percentage of wins logged (and plotted) while the black_model would receive no additional training. As the batches progressed, if the red_model was learning effectively via its training, its win percentage would climb. This is important because in an implementation like this, the loss function does not decline over time as the model learns. So the main metric for improved performance is a win percentage that improes over time with the model that is being trained vs. the model that is not.

However, the goal with this (as it was with AlphaGo) is to train the model on increasingly better opponents. In this case, when the red_model was winning more than 70% of games on a rolling 10-batch average versus the black_model, the bootstrap framework would save red_model‘s parameters and load them into the black model. At that point, the win percentage would drop again to roughly 50%. But as the red_model continued its training, it would continue to improve over its improved but fixed twin, until reaching 70% again, at which point its parameters would be saved to the black model again.

Doing things this way would enable the model to focus on increasingly competitive board positions and presumably on winning in those increasingly competitive situations.

There are reasons I suspected that this approach would be limited, given the model itself and the training methodology. First, the model is comically naive, a simple five-layer fully connected network with a maximum of 1024 neurons in the largest layer. Frankly, I wasn’t sure how much such a model would be able to learn compared to a convolutional net, which I believe would be far more powerful and effective in this situation.

Also, this is simply training the policy distribution on in-game moves. My research has informed me that a better way to do this includes a few important enhancements.

There should be a value output as well as a policy distribution output for the network. I already have the policy distribution: of all the legal moves, which one has the highest probability of leading to a win. I do not have a value output though. The value output for any board position provides an estimate of the probability of winning the game from that position. Training should use Monte Carlo Tree Search (MCTS) simulations from each board position. The MCTS is managed by an Upper Confidence Bound (UCB). This uses both value an policyas well as some other parameters. The model trains the policy network using a cross entropy loss function to predict the actions that are most traversed as part of MCTS using. It trains the value network using mean squared error loss on every board position with a 1 assigned as a target for board positions that were part of winning games and 0 target for board positions that were part of losing games.

All that said, I used this basic policy training to test the performance of the simplistic model. I got some unexpected results. What I was expecting was that the model would get to a 70% rolling win rate relatively quickly when starting from its initialized state and learning against an opponent that remained in an initialized state (version 0). I also expected that as the model played against increasingly trained versions of itself, that it would take longer and longer to get to 70%. The primary reason I expected this was that as the model became increasingly saturated with information about moves with a high probability for success, it would take it longer and longer to go from ~50% wins to 70% wins.

But here is what happened.

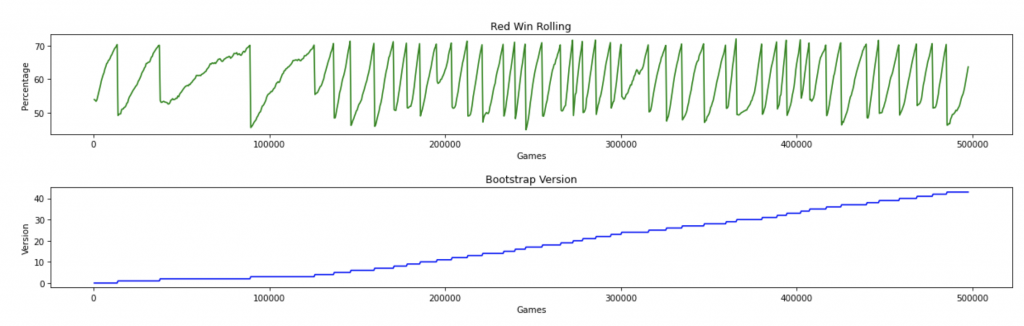
The top graph is the rolling average win percentage for the red_model. The bottom graph shows which version the opponent was on. Each time the win percentage gets to 70%, the black model is updated with the red_model‘s latest values. At that point, the rolling average is cleared and begins ascending from about 50% again, leading to the saw-tooth shape. At each sawtooth drop, the blue line reflects that the version number of the opponent has been increased by 1 because it was updated with the lates parameters from the red_model.

For the first three versions, we can see that the number of batches to get to 70% increases progressively. This was exactly as expected as the model took longer and longer to learn as it became more saturated. But looking at the graph, the model was actually quicker to get to 70% on the fourth version compared to the third. And then, from the fifth version on, it gets to 70% alarmingly quickly each time. In most cases, it does so even quicker than against version 0.

I do not believe the model is actually learning as much as quickly as this graph would seem to indicate. I suspect that what this actually shows is the model getting to some cut-off point beyond which it is actually not learning anything new. I can’t say why this would lead to getting so quickly to 70% over and over again, but my hypothesis is that it is learning some simple and effective technique to beat the current black_model version while probably forgetting a lot that it knew that wasn’t necessary for the previous black_model version.

But that’s just a guess. Right now I can’t verify this one way or the other. My current framework only saves the most recent red_model and the most recent black_model. I am going to need to make a framework that saves every prior version of the black_model and the most recent red_model. I will then need to load each version of the black_model and have the most recent, fully trained red_model play 1,000 games against each successive version of the black_model and log the win percentage of each. If the fully trained red_model has continued to learn across all those successive black_models, each successive black_model should yield lower and lower win percentages for the red_model.

I’m betting that’s not what happens.

Update

One thing occurred to me. What I think may be going on is simply the model getting to the point where it is over-fitting to the opponent. I have not been decreasing the learning rate. I have now set things up to capture each version of the black_model. The training is going on now, but I also added some code to halve the learning rate after each version bump.